Louvain-Performance and Self-Loops

In phase 2 of each pass, the Louvain algorithm creates a collapsed version G’ of the current clustering G. Nodes in a community C in G are represented as a single vertex V_c in G’. Information about the weights of intra-community edges in C in G is preserved in a self-loop edge: (V_c, V_c), where the weight of (V_c, V_c) is equal to the sum of the weights of all edges in C. In subsequent passes, the Louvain-modularity algorithm uses the self-loop weights in its calculations. That is, self-loops count as intra-community weight in the graph created at the start of every pass, in which every vertex is its own community. In this way, self-loop weights actually play a very significant role in these calculations.

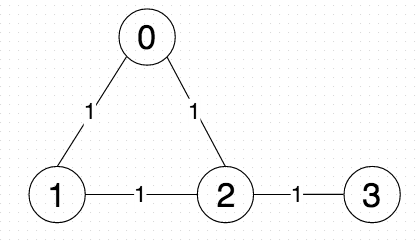
Unfortunately, the performance metric doesn’t account for self-loops. This causes a significant problem; in a connected graph, Louvain-performance will, on each pass, always see improvement by adding vertices to clusterings. By ignoring self-loops, Louvain-performance does not know when to stop clustering, and will result in putting all the vertices into one community. For example, take the graph G:

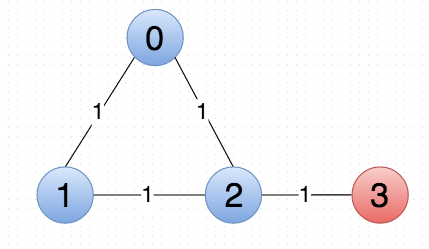
The intuitive clustering, and in fact the clustering that gives maximized performance (0.83, where the meaningful maximum M=1) is where nodes 0, 1, and 2 are in one community, and 3 is a singleton:

Running the current implementation of Louvain-performance gives the following debug information to the command line:

Number of nodes: 4
Number of edges: 4

Running Louvain algorithm...
 num/denom 2.0/6.0
 4 communities:
 0 0
 1 1
 2 2
 3 3

Performance of unaltered graph: 0.3333333333333333
 runLouvainAlgorithm() called
 runLocalMovingAlgorithm() called
   move 0 into 1: 0.16666666666666666
   move 0 into 2: 0.16666666666666666
   MOVING 0 from 0 to 1: 0.16666666666666666
   move 3 into 2: 0.16666666666666666
   MOVING 3 from 3 to 2: 0.16666666666666666
   move 1 into 1: 0.16666666666666666
   move 1 into 2: 0.0
   NO MOVE
   move 2 into 1: 0.3333333333333333
   move 2 into 2: 0.16666666666666666
   MOVING 2 from 2 to 1: 0.3333333333333333
   move 0 into 1: 0.3333333333333333
   NO MOVE
   move 3 into 1: -0.16666666666666666
   NO MOVE
   move 1 into 1: 0.3333333333333333
   NO MOVE
   after updating clusters
   num/denom 5.0/6.0
   2 communities:
   0 0
   1 0
   2 0
   3 1
   perf: 0.8333333333333334

runLouvainAlgorithm() called
runLocalMovingAlgorithm() called
  move 0 into 1: 1.0
  MOVING 0 from 0 to 1: 1.0
  move 1 into 1: 1.0
  NO MOVE
  after updating clusters
  num/denom 1.0/1.0
  1 communities:
  0 0
  1 0
  perf: 1.0
runLouvainAlgorithm() called
  merging clusterings
  num/denom 4.0/6.0
  1 communities:
  0 0
  1 0
  2 0
  3 0
  Performance: 0.6667
 

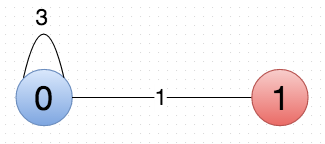
Notice that pass 1 correctly identifies the intuitive clustering (highlighted in blue). Now, the algorithm creates the condensed graph G’:

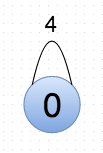
Pass 2 now looks at this data and, unfortunately, performance can’t handle the self-loop (0,0), w((0,0)) = 3. It does the evaluations highlighted in red above, concluding (correctly, if the self-loop didn’t exist) that it should lump vertices 0 and 1 in G’ together. The algorithm concludes that the best clustering is G”, below (but stops short of evaluating on G”, as it only has one node and that would be fruitless):

In the section highlighted in green above, the algorithm is “unraveling” its decisions, and merging later clustering decisions into earlier ones. The final output shows that all the nodes are in the same community (community 0), and performance is the decidedly non-optimal 0.6667.

In order to run Louvain-performance, we must consider creating a modified version of performance that deals with self-loops. In my next post, I will discuss my attempts to modify the metric and its tie-ins to the meaningful maximum M.