Louvain Method Based on the Silhouette Index Metric

Anastasia and I recently finished implementing the Louvain algorithm based on the silhouette index (SI) metric. This post discusses our process.

For a full implementation of any metric in the Louvain algorithm, the algorithm must be able to

1. calculate the metric score of a graph and
2. calculate the change in the metric score of a graph when a vertex is moved to a different community

Part (1) was simply an application of the SI formula. We used the paper by Slobodan Petrović for the detailed description of the metric and the Floyd-Warshall algorithm found at Geeks for Geeks to compute the distance matrix required by the metric.

There are two main differences of the SI implementation of part (2) from the original modularity-based Louvain algorithm. The first is that we implemented part (2) such that the algorithm computes the SI score of the graph before a vertex is moved and again after the vertex is moved rather than depend on a formula that directly calculates the change. Though we lost the speed-up that a change in SI formula would provide, our implementation was more straightforward.

The other difference comes from the initial tie-breaking step. Initially, the Louvain algorithm sets every vertex as its own community, where we will call this the initial state. The SI score of this initial state is 0. When a randomly selected vertex is moved to a different community from this initial state of the graph, the SI score will remain at 0. Since there is no change in the SI score and the original tie-breaking step keeps the vertex in its original community, the graph is stuck in its initial state.

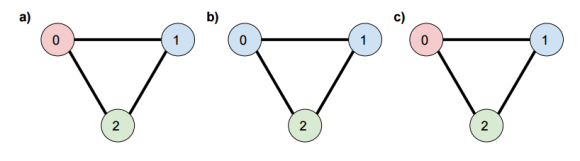
Different communities are represented by different colors. a) Initially, every vertex is in its own community, and the silhouette index score of this state is 0. b) In the first pass of the algorithm, the randomly chosen vertex 0 is moved to community blue, and the silhouette index score of this state is 0. c) There is no change in the metric score, so the algorithm will keep vertex 0 in community red.

To move the graph past its initial state, we force the first randomly chosen vertex to move to a different community. Thus, the next metric score is calculated as if this vertex is in its new community, rather than the community of the initial state.  Note that this tie-breaking step only occurs initially, and the rest of the ties are broken consistent to the modularity-based Louvain algorithm, so this will not affect our analysis between the modularity- and SI-based Louvain algorithm.