CNM Algorithm

At our meeting on 09/18/15, we discussed the two algorithms (Louvain and CNM) that we’ll be investigating this year. I presented on the CNM algorithm, as described in Clauset, Newman, and Moore’s paper “Finding community structure in very large networks.”

Just like the Louvain algorithm, the CNM algorithm uses modularity as its metric and goal. That is, it is constructed to maximize the modularity score, Q.

It does this by keeping track of all the potential combinations of 2 communities and their effects on Q. On every iteration, the algorithm (1) combines the 2 communities whose merge would result in the largest increase in Q, and (2) updates the information about potential combinations and effects on Q. The algorithm terminates when no combination of 2 communities would result in a higher Q.

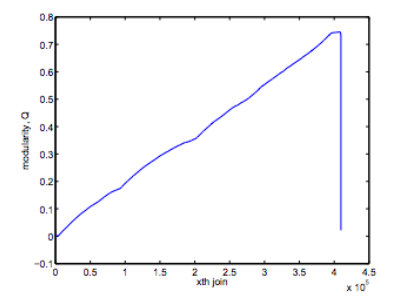
This graph demonstrates how Q reaches a maximum over the course of the algorithm’s execution:

From the data structures side, a sparse matrix keeps track of the potential increases in Q. Each row of the matrix is internally implemented as a balanced binary tree. A max-heap contains the largest element of every row of the sparse matrix, and a vector array keeps track of the fraction of ends of edges that are attached to vertices in a given community i. 

We will explore the CNM algorithm more in depth, and with respect to non-modularity quality measures, after we complete modifications of the Louvain algorithm.